E-News December 2017 Edition

Control Engineering: A Universal Technology

Control Engineers have a capability that few others possess which is the ability to learn from applications experience in an industrial sector and to be able to apply the same solution in what appears a vastly different problem

One of the great benefits of being a control engineer is that the control techniques are applicable to such a wide range of different applications. An example, which is often provided on the ISC training courses for company engineers, is that of ship positioning systems and the relationship to a metal processing control problem.

To explain the point, first consider the control of a dynamically positioned vessel such as an oilrig-drilling vessel, a mine hunter or a firefighting vessel. These are provided with thrusters which enable the position of the vessel to be controlled. The design of a position control for the surge, sway and yaw motions of a vessel would be relatively straight forward, given good measurements. However, the dynamic position (DP) system need not keep the vessel stationary. If it were to attempt to do so it would waste energy and wear out the thrusters. There is no need to oppose the first order wave motion, which would cause continuous cycling of the thrusters. What is required is just to offset the effect of the low frequency forces stemming from the second order wave forces, current forces and low frequency wind disturbances.

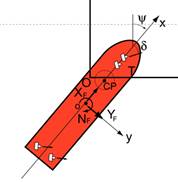
The solution to this problem is to model the ship dynamics and both the high and low frequency disturbance effects and to use a Kalman filter to estimate the model states. The states corresponding to the low frequency motions of the vessel are the ones which must be controlled and involve feedback control action. The states concerning the high frequency motions do not need offsetting and do not require feedback control. The key requirement is therefore the Kalman filter to separate the two types of motion so that different control action can be taken, depending upon the nature of the disturbance. Most advanced ship positioning systems are based upon this principle and the Kalman filter has proved to be a reliable and accurate predictor of motion.

Now consider a steel rolling mill problem.

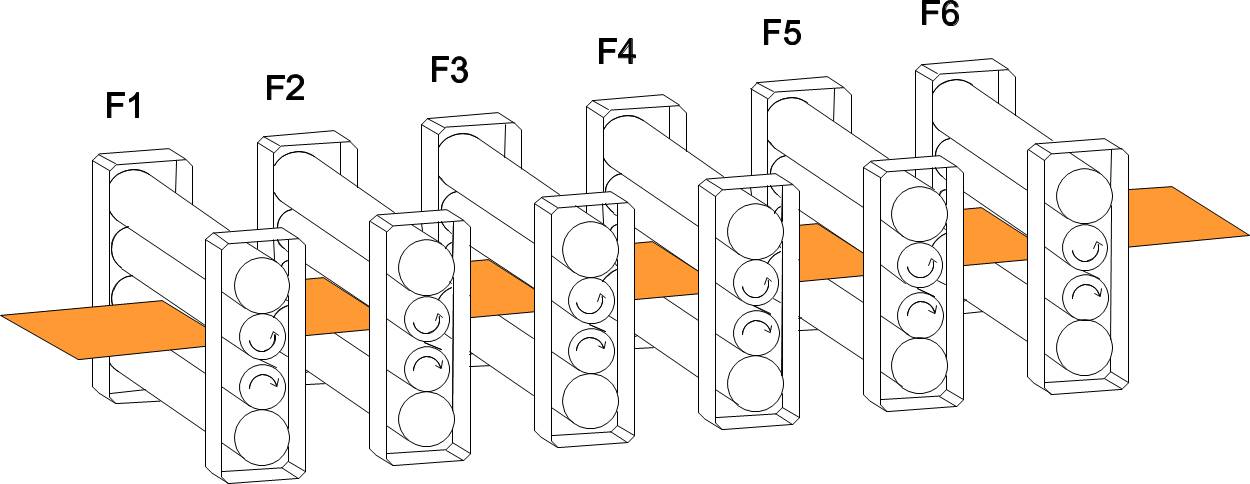
The steel slab is often heated in a reheat furnace to bring the slab up to the correct temperature. This is then rolled in roughing mills before entering a hot strip mill. Unfortunately, when the slab is in the reheat furnace the point at which the slab rests on the rolls is a little colder than for the rest of the slab. The consequence is that when the slab is being rolled in a roughing mill there are areas of higher yield stress, because of the lower temperature, and this leads to slightly larger output thickness from the stand.

This is particularly important in the hot finishing mill when the quality of the product is important. Many hot strip mills control roll force and if the force increases due to an increased input gauge or hardness, then the requirement for the control system is to increase the load to compensate for the inevitable stretch of the mill, so that the resulting output gauge is unchanged. This system is referred to as the gauge meter principle and is widely used.

Unfortunately, there is a second type of disturbance due to the fact that the backup rolls of the mill are not absolutely circular. This can be caused by the roll centres not being exact during the regrinding process or it can be due to cooling sprays when the mill is stopped so that part of the roll is cooled more than the rest of the roll. The eccentricity that results causes a high frequency variation in the strip thickness.

This variation due to eccentricity is amplified by the fact that when the roll force increases die to the roll gap becoming narrower the gauge meter control screws the rolls together, thinking that this is due to input thickness and hardness variations. This is of course the opposite of what is required to maintain a uniform output thickness. That is, for increased hardness and thickness of strip entering the mill when the roll force increases the control system should increase the force even more to compensate for the stretch of the mill. However, if the roll force increases due to eccentricity, this is an indication the roll gap is narrower and the rolls need to be moved apart by reducing the total roll force. Clearly the opposite action on roll force is required depending upon the source of the disturbance.

When this system is modelled, it appears very similar to the ship-positioning problem. The thickness and hardness variations due to the reheat-furnace temperature control problem have relatively slow disturbance effects, by the time the strip reaches the finishing mill. On the other hand the eccentricity effect depends upon the rotational speed of the roll which leads to a high frequency variation. Just as in the ship-positioning problem, a Kalman filter can be used to separate out the different types of motion. There are then a number of options in how the control system is designed. For example, the aim may be to counter the eccentricity disturbance completely or it can be to simply ignore the eccentricity and not make the natural eccentricity worse. In either event, the Kalman filter provides the state estimates providing the crucial separation of the disturbance effects.

It is of course critical to the design of the Kalman estimator that the different types of disturbance have different frequency response characteristics. It is the models of these disturbances, which are involved in the Kalman filter, which enable the motions or variations to be separated.

The main message from the above is that the control engineer is in a very privileged position of being able to derive standard solutions to problems which apply in very different industrial sectors. The experience of industrial systems and control ltd. (ISC Ltd.), across industrial sectors, is its main strength when asked to provide solution to difficult control design solutions.

Acknowledgement and Thanks:
* Redundancy in Dynamic Positioning (DP) Applications based on Satellite Navigation ,High Precision Navigation and Positioning Conference, June 10 2008, O. Ørpen, Fugro Seastar.
* Pressing, Cooling and Coiling - China Steel HSM #1 Major Upgrade Project, Wlodzimierz Filipczyk, Sr. Systems/Application Engineer - TM GE Automation, Salem, VA ,1501 Roanoke Blvd , Salem, Va. 24153 - USA

Mike Grimble

Top

Dr Shuo Zhang has joined our team at ISC in Glasgow

Dr Shuo Zhang has joined our team of control engineering consultants at ISC in Glasgow. Shuo completed his Masters degrees in Control Theory and Control Engineering at Beijing Institute of Technology and moved to the Netherlands to complete his PhD at the University of Groningen on methods for characterising the dynamics in multi-agent networks, as well as sitting many DISC courses in advanced control methods. He has worked for Siemens Wind Power in the UK for the last 4 years on power conversion control and its interaction with the AC grid. He has an excellent blend of deep theoretical knowledge of classical/advanced control and the practical needs when translating into real-world applications. He is looking forward to working on novel and challenging control applications that we tend to look at here at ISC. We are very glad to have Shuo, and welcome him to ISC!

Top

Linear Matrix Inequalities

A design method involving linear matrix inequalities (LMI's) may sound rather advanced and not very practical for real applications. However, the name stems from the origin of a numerical algorithm and the actual use and application can be relatively straightforward. Such problems were difficult to solve but the mathematics is now hidden below the surface of the user-friendly university software (like Yalmip), or commercial LMI toolboxes (Matlab Robust Control Toolbox). The problem today is therefore to represent the system design requirement in the terms needed by the software tool.

One of the most intransigent problems in control design is that of achieving real robustness, which is very illusive. It seems that when the gift of robustness was handed out to different design methods the old PID controller took more than its fair share and left all of the other methods with varying levels of robustness problem.

There is of course a little exaggeration here but in general, advanced control methods provide good performance but not necessarily good robustness in their basic form. The LMI approach enables this problem to be addressed in a scientific way using well-established and well-developed numerical algorithms.

The solutions too many problems in control or indeed signal processing, can be found if they can be represented as a set of linear matrix equations involving inequalities. The uncertainties, which arise in modelling industrial plants, can of course often be described using matrix inequalities and this enables optimal controllers to be derived to minimise both the cost-function and satisfy uncertainty bounds.

In fact, many of the standard problems in control such as model predictive control, linear quadratic regulators, linear quadratic Gaussian, Lyapunov equations, Riccati equations and H? designs can be expressed in such a manner, and solved by this type of software. Optimization problems that are computationally di?cult can often be approximated by LMI problems.

The main message here is not to be put off by the rather unfamiliar mathematics, which underpins the methods but instead focus upon the use of the design software, which is not so daunting.

For further details or questions contact Professor Mike J Grimble.

Forthcoming ISC Training Courses

6th - 8th March 2018
Control Fundamentals

9th May 2018
Introduction to Process Control

11th & 12th Sept 2018
System Identification

20th & 21st Nov 2018
Optimisation and Model Predictive Control for Linear Systems

If you would like further details or to register interest on any of these courses please contact Dr Meghan McGookin.

Top

Receding Horizon and Predictive Control

Key to the idea of a predictive control system is the receding horizon principle. This involves computing on an optimal control trajectory for a prediction horizon and then only implementing the first computed control before going on to the next time step. To explain more clearly most of the predictive control systems assume that future set point information is known and a prediction horizon which might be ten or twenty time steps is defined. The cost function will include tracking errors over this horizon and also the corresponding control actions which may or may not be costed over the same horizon. However, for the present discussion assume the same number of control steps are included in the cost function as those penalising tracking errors (the prediction horizon).

The optimisation algorithm for a predictive control normally computes at a given time t the optimal control to minimise the cost throughout the prediction horizon. This is rather like solving a linear quadratic (LQ) optimal control problem to minimise the cost function. The optimal control throughout the interval will depend upon any future known deterministic disturbance and reference signal and in this sense the control is similar to an open loop control for the system. However, only the initial value of the computed future control trajectory is actually implemented.

At the next time instant the process is repeated and again only the initial value of the computed control trajectory is implemented. This is what is termed the receding horizon principal. It is similar to computing a moving window of controls whilst only implementing the first value.

From a theoretical viewpoint this is not a very sound strategy, even if it works in practise. It means that predictive controls often have good performance in operation but it is very difficult to quantify the robustness and stability properties. If the prediction horizon is rather short the standard model predictive control can have very poor behaviour on non-minimum phase systems when the control costing is small and similarly if the system is open loop and stable poor results will be obtained when the cost weighting is large. Nevertheless, the proof of the pudding is that in most applications reasonable prediction horizons can be found which provide reasonable stability properties and performance.

To try to explain why the receding horizon principle works at all the links with LQ optimal control can be exploited. If the prediction horizon is reasonable long the control computed at each time step by this method will be similar to the LQ optimal control. It is interesting to note that even a finite horizon LQ problem does not have guaranteed stability properties since surprising at it sounds an optimal solution does not ensure stability. This is because when a cost is minimised over a finite time period the problem does not include the information that in the steady state the system should be stable. If an optimal control signal that is unstable will minimise the cost better than that is what the optimal solution will provide.

It is also interesting that although reference above was made to the computation of an open loop control because at each time step new measurements are available the control also has elements of feedback action. This is because new initial conditions for generating the optimal control throughout the prediction horizon apply.

We may therefore conclude predictive control is a very strange beast and its main justification is that is just simply works. It is difficult to argue that such a successfully control has any weaknesses and we therefore commend its use to all.

Top

Book Review: Robust Control Engineering - Practical QFT Solutions, by: Mario Garcia-Sanz, Published By: CRC Press (Taylor & Francis Group), Hardback Cost: £100, eBook Cost: £73.80

Professor Garcia-Sanz is one of the leading exponents of the robust control design method, which is referred to as quantitative feedback theory (QFT). This excellent text introduces the fundamentals of QFT and provides control solutions for a range of systems including unstable, transport delay, non-minimum phase and distributed parameter systems.

The QFT design method provides real robustness to uncertainties of various types. The method originated from the work of Professor Isaac Horowitz but this book extends his original work in many ways. It is particularly valuable for the range of applications considered including wind turbines, wastewater treatment plants, power systems, satellites, radio telescopes and manufacturing systems.

A feature of such design texts is that they often contain MATLAB toolboxes to enable the design methods to be assessed. In this case the book includes problems where the MATLAB QFT control toolbox can be applied. This was developed by the author.

The book is written in a style that should be very accessible to engineers, particularly those that have a classical control engineering background. In fact, it provides access to modern multivariable control design methods but it is based upon frequency response ideas that should be very familiar to most engineers.

The layout of the text is excellent and it includes numerous examples and problems. It should be valuable to experienced engineers working on real control design applications but it is also suitable for undergraduate and graduate students pursuing courses on control engineering. It is recommended for the bookshelves of engineers or the more economical eBook version can be convenient.

Book Nerd.

Top

Book Review: Electronic Instrumentation for Distributed Generation and Power Processes, by: Felix Alberto Farret, Marcelo Godoy Simões, Danilo Iglesias Brandão, Published By: CRC Press (Taylor & Francis Group, Paperback: £50, Hardback: £110, eBook: £45

This text should be valuable to engineers working on both analogue and digital instrumentation systems. It covers many of the main concepts in sensors and transducers and electronic instrumentation. The power system applications area is the focus for the text and particularly distributed generation systems.

The chapter on fuzzy logic and neural networks for distributed systems was of particular interest being rather unusual. The last chapter also stands out and concerns smart grid systems.

This is a rather specialized text, however for engineers working in industry in the general area of power systems it is a very desirable reference work and for students on University courses it provides an excellent intuitive introduction to many engineering topics.

Book Nerd.

Top

Book Review: Linear Continuous-Time Systems by: Lyubomir T. Gruyitch, Published By: CRC Press (Taylor & Francis Group), Hardback Cost: £115, eBook Cost: £103.50

This new text is aimed at linear continuous time, time invariant dynamical systems. The text is very suitable for courses covering system models, mathematical system theory, and stability and design issues. It should be helpful to engineers that require a reference text on continuous systems, since it provides an extensive bibliography and useful appendices. It is probably more value to researchers than to engineers in industry. It is useful for those interested in the mathematics of the subject and it presents some familiar material in a new manner.

Book Nerd.

Top